
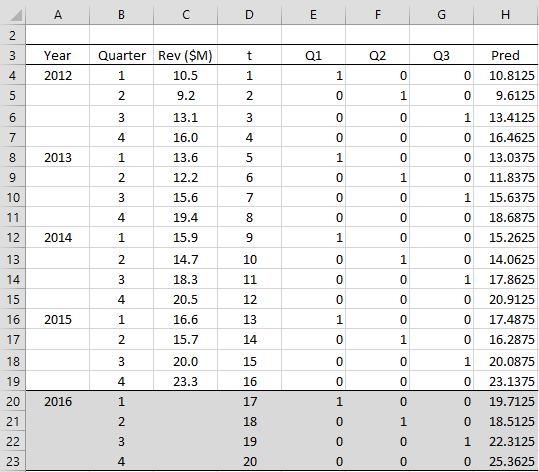
Since I have 4 IVs with high VIF, how can I identify which of the IVs have collinearity with each other? Because it could either be that the 4 IVs are all multicollinear or that 2 sets of the IVs are multicollinear.ģ. What does this mean and how can I interpret it?Ģ. I’m not sure what I’m doing here but what I notice is that the VIF of one of the 3IVs significantly changed after I removed the 4th IV. I ran a regression on these 4 IVs (with high VIF) against the dependent variable and compared it with another regression with 3 IVs (with high VIF) removing one IV to see what happens. I’ve checked the VIF’s and there are 4 IV’s with high VIF (>10 – this is the rule of thumb I am going by). I have a problem case with 16 independent variables (IV). Other webpages that might be helpful are: In particular, you can test what happens to the correlation value when you leave out one or more of the independent variables.This sort of test is described at Thus, you can use all the typical regression approaches. Calculating multiple correlation is equivalent to running a multiple regression and finding the square root of the R-square value. I am not saying that you should do this, especially since it won’t change the correlations, but this is how you can do it.Ģ. You can standardize the scales by using the STANDARDIZE function on the data in each column (i.e. Note that we should be concerned about the Traffic Deaths and University variables since their tolerance values are about. The results are shown in the bottom part of Figure 1. 482 and VIF(C4:J15,3) = 2.07 (since Crime is the 3 rd variable). 482 and VIF = 1/.482 = 2.07.Īlternatively we can use the supplemental functions TOLERANCE(C4:J15,3) =. (To do this we first need to copy the data so that Input X consists of contiguous cells). From these data, we can calculate the Tolerance and VIF for each of the 8 independent variables.įor example, to calculate the Tolerance for Crime we need to run the Regression data analysis tool for the data in the range C4:J15 excluding the E column as the Input X vs. The top part of Figure 2 shows the data for the first 12 states in Example 1. the data for the first 12 states in Example 1 of Multiple Correlation). Observation: TOLERANCE(R1, j) = 1–RSquare(R1, j)Įxample 1: Check the Tolerance and VIF for the data displayed in Figure 1 of Multiple Correlation (i.e. VIF(R1, j) = VIF of the jth variable for the data in range R1 TOLERANCE(R1, j) = Tolerance of the jth variable for the data in range R1 i.e. 1 – Real Statistics Excel Functions: The Real Statistics Resource contains the following two functions: A tolerance value of less than 0.1 is a red alert, while values below 0.2 can be cause for concern. We want a low value of VIF and a high value of tolerance. Observation: Tolerance ranges from 0 to 1.

The variance inflation factor ( VIF) is the reciprocal of the tolerance. the multiple coefficient between x j and all the other independent variables. We now define some metrics that help determine whether such a situation is likely. Even when one column is almost a linear combination of the other columns, an unstable situation can result. Observation: Unfortunately, you can’t always count on one column being an exact linear combination of the others. Then the denominators of the coefficients are zero and so the coefficients are undefined. Observation: In the case where k = 2, the coefficient estimates produced by the least square process turn out to be Excel detects this and creates a regression model equivalent to that obtained by simply eliminating column X2. Such a situation is called multicollinearity, or simply collinearity, and should be avoided.Į.g., in the following table, X1 is double X2. small changes in X may result in significant changes in B and Y-hat. det( X TX) is close to zero, the values of B and Y-hat will be unstable i.e. one independent variable is a non-trivial linear combination of the other independent variables. This occurs when one column in X is a non-trivial linear combination of some other columns in X, i.e.

doesn’t have an inverse (see Matrix Operations), then B won’t be defined, and as a result Y-hat will not be defined. From Definition 3 and Property 1 of Method of Least Squares for Multiple Regression, recall that


 0 kommentar(er)
0 kommentar(er)
